快跨年了，祝大家“好柿连续发生”

快到岁末跨年的时候，脑海里突然蹦出那个“好柿发生”的表情包。好事发生很可贵，好事连续发生更像中了大奖。我当然由衷祝愿每一个人都“好事连续发生”——反正也不用我随份子，我只负责动动嘴皮子。

但问题来了：好事连续发生，真的都值得激动吗？

试想一个场景：你研究了一套投资策略，策略帮你选了一只股票。你买入，然后这只股票从某天开始连续上涨 5 天。这时候，你能放心庆祝“成了”吗？

这个问题，依然可以用贝叶斯方法来分析。今天分享的贝叶斯，会稍微“上点强度”——我们不再囫囵吞枣地拍一个先验概率，而是直接引入一个概率分布来描述不确定性。

概率也会不确定：于是有了“概率的概率”

像“一个投资策略每天胜率在 0～1 之间”这种不确定的数值，本身也可以有一个概率分布来刻画。听上去有点奇特：概率的概率。

但仔细想想这并不玄学：我们说“策略胜率是 55%”，这句话本身就带着不确定性——55% 只是你基于有限样本的判断。世界充满不确定性，甚至“世界充满不确定性”这句话本身也未必绝对成立，挺辩证的。

于是，为了刻画“胜率 (p)”这种落在 ([0,1]) 的未知量，我们需要一种专门的分布：Beta 分布。

如果你对概率论不太熟，这里可能已经开始“不讲人话”了。但别急着走，先抢救一下自己：在处处追求爽感的内容里，能真正磨砺大脑的东西并不多。

概率论里说的“分布”，就是：

一个结果可能取到哪些值，以及每个值出现得有多频繁/有多可能。

比如“身高分布”：大多数人集中在 160–180cm，特别高或特别矮的人很少——这张“多在哪、少在哪”的地图就是分布。

再换个更生活的：周五晚上你打开高德地图看拥堵状况，有的路段红，有的绿，那也是分布。只不过它把“密度/概率”用红绿这种视觉方式表现出来了。

不同形状、不同生成机制的数据，就对应不同的分布。有些分布非常常见，前辈们研究得透透的，甚至写成了标准公式，比如大名鼎鼎的正态分布（高斯分布）。

Beta 分布（贝塔分布）是一种“概率的概率分布”。它不是在描述“硬币正面朝上的结果”，而是在描述：

这枚硬币正面朝上的真实概率 (p) 可能是多少。

你扔了 1000 次硬币，有 501 次正面，算出来正面概率是 50.1%。
那 Beta 分布要回答的不是“这次是不是正面”，而是：

“这枚硬币真实的 (p) 接近 0.501 的可能性有多大？它还可能偏到哪里去？”

不但有点绕，还有点有趣。

简而言之：Beta 分布用来表示一个未知概率 (p\in[0,1]) 的不确定性：

最通俗的理解：(\alpha,\beta) 像你心里的两摞“虚拟记录”。

以硬币为例：

对投资策略也是一样：

由此你能记住四个直觉：

Beta 分布的概率密度曲线就是下面这样：

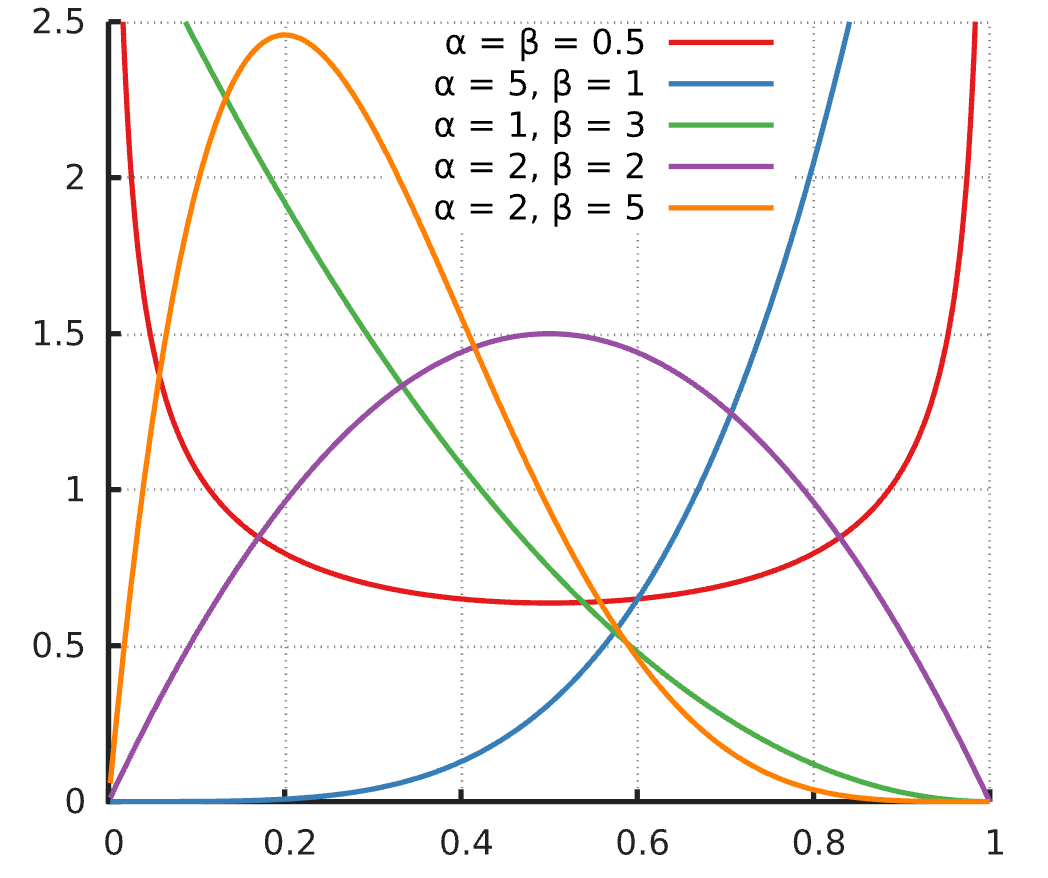
Beta 分布

假设一个策略的胜率（更准确说：每天上涨的概率）用 Beta 分布描述。它已经在线上跑了 1000 天，其中上涨天数是 (\alpha)，下跌天数是 (\beta)，显然 (\alpha+\beta=1000)。

这时策略的“平均胜率”（直觉上的中心）大致是：
[
\frac{\alpha}{\alpha+\beta}
]

然后你遇到新的证据：连续 5 天上涨。贝叶斯更新告诉你：把这 5 次“成功”加进去，新的分布还是 Beta（这叫共轭分布，听不懂也完全没关系，记住结论就行）：

现在关键问题是：新分布相比旧分布，变化大不大？

答案很朴素：主要看你之前“有多久经沙场”。

这两个值差得大不大，几乎完全取决于 (\alpha+\beta) 有多大。

如果你已经跑过 1000 天，那 5 天连涨带来的更新通常很小；
如果你只跑过 10 天，那 5 天连涨就会把你的信念拽着跑。

也就是说：一个策略是否“真的变强了”，不由“连续好事的数量”决定，而由它在此前经历过多少次检验决定。老兵不会因为 5 件好事就自封神，也不会因为 5 件坏事就宣布死亡。

先问样本量：这 5 天发生在多少天的背景上？
- 5/10 和 5/1000 的信息量完全不是一个级别。
把“庆祝/恐慌”换成“更新幅度”：我应该更新多少？**
- 样本小：更新可以大，但要承认“不确定性仍然大”。
- 样本大：更新应当小，更多把它当噪声。
把“突然而至的好事或者坏事”当提醒，而不是结论，应该去检查“机制有没有变”
- 是市场环境变了？
- 交易成本/滑点变了？
- 策略是否偏离了原本适用的 regime？
  连续上涨/下跌本身，往往只是提醒你“该做体检”，而不是直接给出诊断书。